Calibrating a Random Forest Classifier

In the previous blog post , we looked at the probability predictions that come out of naive implementation of the scikit-learn Random Forest classifier. We noted that the predictions are not well-calibrated, but did not address how to fix that problem, which is the subject of this blog post.

Calibrating a Random Forest Classifier

It turns out that calibrating the random forest classifier in scikit-learn is really only a matter of an additional line or two of code, as scikit-learn helpfully comes with a method to do exactly the thing we want: the CalibratedClassifierCV class. This class uses a train set to fit the original method, and then uses a test set to calibrate the probabilities afterwards. Note that it works for any classifier method in the scikit package, not just for random forest.

There are two methods for calibration available in this class - isotonic and sigmoid. The sigmoid method corresponds to something called Platt’s Method or Platt’s scaling. This method essentially fits a logistic regression to the output of the original classifier. According to the Wikipedia article

Platt scaling has been shown to be effective for SVMs as well as other types of classification models, including boosted models and even naive Bayes classifiers, which produce distorted probability distributions. It is particularly effective for max-margin methods such as SVMs and boosted trees, which show sigmoidal distortions in their predicted probabilities, but has less of an effect with well-calibrated models such as logistic regression, multilayer perceptrons, and random forests.

I was interested to note that this particular Wikipedia article considers random forest models to be well-calibrated! (I don’t.)

What we’ll be using in this example, though, is the isotonic method, which is a non-parametric method that works well if there is sufficient data in the test set.

Show me

The notebook with the full code is available here.

Create classification data

As before, we’ll start by creating some classification data.

X, y = make_classification(n_samples=20000, n_features=3, n_informative=3, n_redundant=0, random_state=0, shuffle=False)

Train a random forest both with and without CalibratedClassifierCV.

Split the data into train and test sets:

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

Random forest trained with no calibration:

clf = RandomForestClassifier(max_depth=3, random_state=0, min_samples_leaf=3).fit(X_train, y_train)
predictions_rf = clf.predict_proba(X_test)

Random forest trained with CalibratedClassifierCV:

clf = RandomForestClassifier(max_depth=3, random_state=0, min_samples_leaf=3)
clf_isotonic = CalibratedClassifierCV(clf, method='isotonic')
clf_isotonic.fit(X_train, y_train)
predictions_isotonic = clf_isotonic.predict_proba(X_test)

Bin the predictions and plot the two sets of predictions

We can see that the curve corresponding to the isotonic calibration now tracks much closer to the x=y line (which would indicate perfect calibration). It’s not perfect, but it’s much better than probability predictions coming out of the uncalibrated random forest classifier. Note especially how much better it does at the high and low ends of the calibration curve.

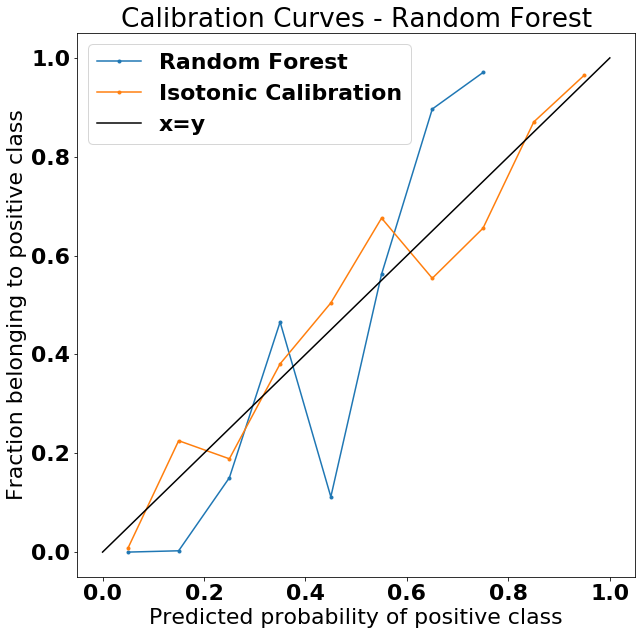
We can also get a numerical estimate of how much better we’re doing by using the Brier’s Score, which is really just the mean squared error of the predicted probabilities.

print("Brier scores: (smaller is better)")

clf_score = brier_score_loss(y_test, predictions_rf[:,1])
print("No calibration: %1.3f" % clf_score)

clf_isotonic_score = brier_score_loss(y_test, predictions_isotonic[:,1])
print("With isotonic calibration: %1.3f" % clf_isotonic_score)

The output of this score for these two models is

Brier scores: (smaller is better)
No calibration: 0.152
With isotonic calibration: 0.094

Which confirms what we can also see by eye in the plot above–the calibrated random forest produces better probability estimates.

Conclusion

In this two-part blog post, we’ve seen that, on its own, the random forest classifier poorly calibrated. Luckily, it’s only a matter of another two lines of code to get the well-calibrated random forest classifier of your dreams.